The study of suborbital graphs is a key area in group theory for it provides a graphical representation of a group action on a set. Moreover, it helps in understanding the combinatorial structures of the action of a group on a set. In this paper, we construct suborbital graphs based on the group action of the direct product of the symmetric group on Cartesian product of three sets through computation of the ranks and subdegrees of the group action. Suborbital graphs are constructed by the use of Sims theorem. The properties of the suborbital graphs are analyzed. In the study it is proven that the rank of the group action of direct product of the symmetric group acting on the Cartesian product of three sets is 8 for all n ≥ 2 and the suborbits are length 1, (n-1), (n-1), (n-1), (n-1)2, (n-1)2, (n-1)2, (n-1)3. We show that the suborbits of the group action are self-paired. Furthermore, it is demostrated that each graph has a girth of 3 for all n > 2 and suborbital graphs of the group action are undirected. It is shown that graphs Γ2 and Γ3 are regular of degree n-1, graphs Γ4, Γ5 and Γ6 of degree (n-1)2 and graph Γ7 is regular of degree (n-1)3. The suborbital graphs Γi(i=1, 2,…, 6) are disconnected, with the number of connected components equal to n2 while suborbital graph Γ7 is connected for all n > 2.
| Published in | American Journal of Applied Mathematics (Volume 12, Issue 5) |
| DOI | 10.11648/j.ajam.20241205.17 |
| Page(s) | 175-182 |
| Creative Commons |
This is an Open Access article, distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution and reproduction in any medium or format, provided the original work is properly cited. |
| Copyright |
Copyright © The Author(s), 2024. Published by Science Publishing Group |
Rank, Subdegrees, Suborbit, Suborbital Graphs
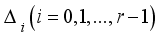 correspond to the suborbital . Then is undirected if is self-paired and is directed if is not self-paired
correspond to the suborbital . Then is undirected if is self-paired and is directed if is not self-paired Suborbit | Formula | Number of suborbits |
|---|---|---|
Orbit comprising no element from | 3C0 | 1 |
Orbits comprising a single element from | 3C1 | 3 |
Orbits comprising two elements from | 3C2 | 3 |
Orbit comprising three elements from | 3C3 | 1 |
Suborbit length | 1 |
|
|
|
|---|---|---|---|---|
number of suborbits | 1 | 3 | 3 | 1 |
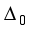 is a null graph. The remaining suborbits are self- paired. Consider for the example
is a null graph. The remaining suborbits are self- paired. Consider for the example 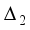 = {(1, 4, 5)}for.
= {(1, 4, 5)}for. 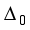 is a null graph and the remaining seven suborbital graphs are given as follows;
is a null graph and the remaining seven suborbital graphs are given as follows; 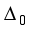 is a null graph and the remaining seven suborbital graphs of S3×S3×S3 Acting on X×Y×Z are given as follows;
is a null graph and the remaining seven suborbital graphs of S3×S3×S3 Acting on X×Y×Z are given as follows;
| The Suborbit of G on X |
|
|
| The Suborbital Graph Corresponding to the Suborbit |
|
|
| External direct product of |
| [1] |
Cameron, P. J., Gewurz, D. A., and Merola, F. (2008). Product action. Discrete Math. 386–94.
https://www.sciencedirect.com/science/article/pii/S0012365X07003810 |
| [2] |
Harary, F. (1969). Graph Theory. Addison-Wesley Publishing Company, New York.
https://www.sciencedirect.com/science/article/abs/pii/0378873383900266 |
| [3] | Muriuki, G. D., Namu, N. L., & Kagwiria, R. J. (2017). Ranks, sub degrees and suborbital graphs of direct product of the symmetric group acting on the cartesian product of three sets. Pure and Applied Mathematics Journal, 6(1), 1. |
| [4] | Nyaga, L. N. (2012). Ranks, Subdegrees and Suborbital Graphs of the Symmetric Group Sn Acting on Unordered r−Element Subsets. PhD thesis, JKUAT, Juja, Kenya. |
| [5] | Rimberia, J. K. (2011). Ranks and Subdegrees of the Symmetric Group Sn Acting on Ordered r− Element Subsets. PhD thesis, Kenyatta University, Nairobi, Kenya. |
| [6] | Rose, J. S. (1978). A Course in Group Theory. Cambridge University Press, Cambridge. |
| [7] | Sims, C. C. (1967). Graphs and finite permutation groups. Mathematische Zeitschrift, 95: 76–86. |
| [8] | Wielandt, H. (1964). Finite Permutation Groups. Academic Press New York. |
APA Style
Muriuki, G. D., Namu, N. L. (2024). Suborbital Graphs of Direct Product of the Symmetric Group Acting on the Cartesian Product of Three Sets. American Journal of Applied Mathematics, 12(5), 175-182. https://doi.org/10.11648/j.ajam.20241205.17
ACS Style
Muriuki, G. D.; Namu, N. L. Suborbital Graphs of Direct Product of the Symmetric Group Acting on the Cartesian Product of Three Sets. Am. J. Appl. Math. 2024, 12(5), 175-182. doi: 10.11648/j.ajam.20241205.17
AMA Style
Muriuki GD, Namu NL. Suborbital Graphs of Direct Product of the Symmetric Group Acting on the Cartesian Product of Three Sets. Am J Appl Math. 2024;12(5):175-182. doi: 10.11648/j.ajam.20241205.17
@article{10.11648/j.ajam.20241205.17,
author = {Gikunju David Muriuki and Nyaga Lewis Namu},
title = {Suborbital Graphs of Direct Product of the Symmetric Group Acting on the Cartesian Product of Three Sets
},
journal = {American Journal of Applied Mathematics},
volume = {12},
number = {5},
pages = {175-182},
doi = {10.11648/j.ajam.20241205.17},
url = {https://doi.org/10.11648/j.ajam.20241205.17},
eprint = {https://article.sciencepublishinggroup.com/pdf/10.11648.j.ajam.20241205.17},
abstract = {The study of suborbital graphs is a key area in group theory for it provides a graphical representation of a group action on a set. Moreover, it helps in understanding the combinatorial structures of the action of a group on a set. In this paper, we construct suborbital graphs based on the group action of the direct product of the symmetric group on Cartesian product of three sets through computation of the ranks and subdegrees of the group action. Suborbital graphs are constructed by the use of Sims theorem. The properties of the suborbital graphs are analyzed. In the study it is proven that the rank of the group action of direct product of the symmetric group acting on the Cartesian product of three sets is 8 for all n ≥ 2 and the suborbits are length 1, (n-1), (n-1), (n-1), (n-1)2, (n-1)2, (n-1)2, (n-1)3. We show that the suborbits of the group action are self-paired. Furthermore, it is demostrated that each graph has a girth of 3 for all n > 2 and suborbital graphs of the group action are undirected. It is shown that graphs Γ2 and Γ3 are regular of degree n-1, graphs Γ4, Γ5 and Γ6 of degree (n-1)2 and graph Γ7 is regular of degree (n-1)3. The suborbital graphs Γi(i=1, 2,…, 6) are disconnected, with the number of connected components equal to n2 while suborbital graph Γ7 is connected for all n > 2.
},
year = {2024}
}
TY - JOUR T1 - Suborbital Graphs of Direct Product of the Symmetric Group Acting on the Cartesian Product of Three Sets AU - Gikunju David Muriuki AU - Nyaga Lewis Namu Y1 - 2024/10/18 PY - 2024 N1 - https://doi.org/10.11648/j.ajam.20241205.17 DO - 10.11648/j.ajam.20241205.17 T2 - American Journal of Applied Mathematics JF - American Journal of Applied Mathematics JO - American Journal of Applied Mathematics SP - 175 EP - 182 PB - Science Publishing Group SN - 2330-006X UR - https://doi.org/10.11648/j.ajam.20241205.17 AB - The study of suborbital graphs is a key area in group theory for it provides a graphical representation of a group action on a set. Moreover, it helps in understanding the combinatorial structures of the action of a group on a set. In this paper, we construct suborbital graphs based on the group action of the direct product of the symmetric group on Cartesian product of three sets through computation of the ranks and subdegrees of the group action. Suborbital graphs are constructed by the use of Sims theorem. The properties of the suborbital graphs are analyzed. In the study it is proven that the rank of the group action of direct product of the symmetric group acting on the Cartesian product of three sets is 8 for all n ≥ 2 and the suborbits are length 1, (n-1), (n-1), (n-1), (n-1)2, (n-1)2, (n-1)2, (n-1)3. We show that the suborbits of the group action are self-paired. Furthermore, it is demostrated that each graph has a girth of 3 for all n > 2 and suborbital graphs of the group action are undirected. It is shown that graphs Γ2 and Γ3 are regular of degree n-1, graphs Γ4, Γ5 and Γ6 of degree (n-1)2 and graph Γ7 is regular of degree (n-1)3. The suborbital graphs Γi(i=1, 2,…, 6) are disconnected, with the number of connected components equal to n2 while suborbital graph Γ7 is connected for all n > 2. VL - 12 IS - 5 ER -